・一次反応

まずは一番単純な，
　 Ａという物質がＢという物質にランダムに，確率的に変化する
という反応です．
ここで重要なポイントは，
　 ランダム
　 確率的
という点です．
ここに協調性などが入ってくるとややこしくなりますね．
では，”変化”とは何か？
何でもいいです．
物質の状態そのままでもいいし，
　 蛍光の退色
　 原子の崩壊
でも何でもいいのです．

さて，ある濃度のＡ溶液があるとします．
時間とともに，ＡがＢに変わっていくわけです．

ここでのポイントは，
　 Ａ＋Ｂは一定
　 Ｂの濃度の上昇率（Ａの濃度の減少率）はＡの濃度に比例する
　 その比例定数，k，は一定
です．
考えている世界にはＡとＢしかありませんから，その総量は一定です．
Ａはそれぞれ独立に変化しますので，Ａの濃度（数）が多ければ，Ｂの濃度（数）の上昇率，もしくは，Ａの濃度の減少率は上がります．
そして，その比例定数は一定（温度が一定なら）とします．

これを式で表すと，

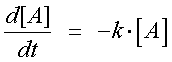
となります．
式の左はＡの濃度の変化率，右はその際のＡの濃度となります．
定常状態においては，左辺の時間変化が０になりますので，
[A]=0，となり，Ａの濃度はいずれは０となります．
過渡的にはどうなるかというと，あるものを微分すると，同じものが出てくるのは指数関数の典型例ですので，この式を解くと，

となります．
ここで，Ｃ，は未知の定数ですね．
この，Ｃ，を求めるには，初期値を導入する必要があります．
では，初期値(t=0)において，
　 [A]=[A0], [B]=0
を考えます．
最初はすべてＡという意味ですね．
となると，t=0において，

となり，

となります．
つまり，Ａの濃度は指数関数的に減少するわけです．

では，Ｂの濃度はどうなるでしょう？
　 [A0]=[A]+[B]
ですので，

となり，指数関数的に上昇します．

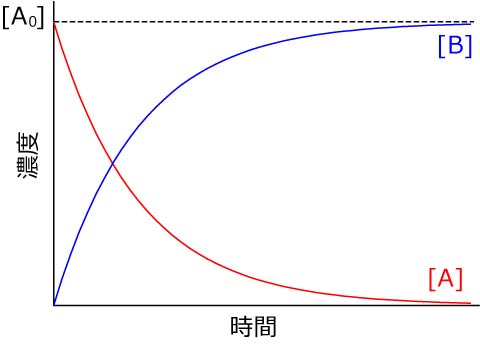
この反応で重要なのは，
　 濃度が半減する時間は初期濃度に依存しない
というものです．
これをきちんと数式で表すと，濃度が半減，というものは，
　 [A0]/2
ですね，それにかかる時間は，

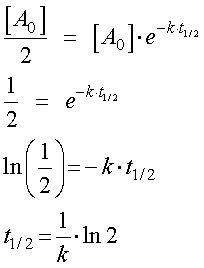
となり，初期濃度，A0に依存しないことになります．

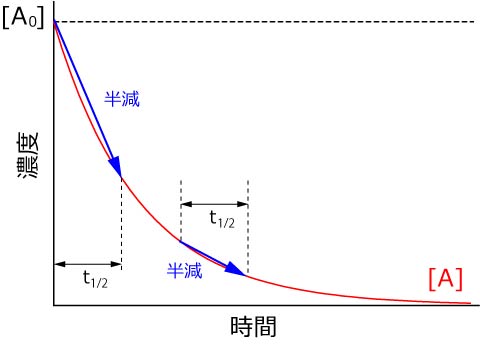
つまり，このような単純な一次反応の場合，速度定数，k，を求めるには，初期濃度を厳密にコントロールする必要はないのです．
最初の濃度，[A0]，がいくらでもいいし，反応生成物，B，が存在してもかまいません．

では，一個一個の分子を見た場合にはどうなるでしょう？
　 A -> B
上の式と違うのは濃度を示す，括弧，がないことですね．
これはエルゴード性，時間平均と数の平均は等しくなる，という仮定から得られるとのことです（ここは勉強不足ですので，厳密には正しくないかもしれません）．
ですので，一個一個の分子の変化の時間を見てもその分布は指数関数的になるということです．
つまり，とっても早く変化する分子がいっぱいいて，ゆっくり変化する分子はどんどん少なくなってくる，その分布は指数関数的である，ということですね．

次は二次反応です．